Matplotlib (und IPython und Jupyter Notebooks)¶
Notizen¶
Matplotlib ist ein umfangreiches und mächtiges Programmpaket zur Plotten von Daten. In den meisten Python-Distributionen, die für den Einsatz in der Wissenschaft konzipiert sind, ist es bereits enthalten. Die offizielle Dokumentation finden Sie hier, und ein sehr gutes Tutorial mit Übungen zum Nachmachen hier.
Ebenfalls nützlich sind die neuen Tutorials auf der Matplotlib-Webseite.
Sehr hilfreich ist auch die Galerie von Beispiel-Plots, in der man für jede Beispielgrafik den Quelltext abrufen kann, mit dem sie erzeugt wurde. Das macht die Modifikation für die eigenen Bedürfnisse sehr einfach.
Ein einfaches Tutorial finden Sie auf hier. Dort können Sie auch die interaktiven IPython-Notebooks jeder Lektion herunterladen.
Das folgende Skript generiert einen Plot mit zwei Graphen und modifiziert einige der default-Eigenschaften.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70
# Standard-Einbindung der Matplotlib-Funktionalitaeten ueber ein MATLAB- # artiges Befehlsinterface. Sehr oft findet man auch die Einbindung mit dem # Synonym plt statt plt. import matplotlib.pyplot as plt import numpy as np # Generierung der "Leinwand", auf der die Plots gezeichnet werden, Ausdehnung # in Zoll, Aufloesung in dpi, Dots per Inch plt.figure(figsize=(8, 6), dpi=80) # Create a new subplot from a grid of 1x1 plt.subplot(1, 1, 1) # x-Werte fuer die beiden Beispielplots als eindimensionales numpy-Array # generieren X = np.linspace(-np.pi, np.pi, 256, endpoint=True) C, S = np.cos(X), np.sin(X) # Und die y-Werte dazu # Plot cosine with a blue continuous line of width 1 (pixels) ##plt.plot(X, C, color="blue", linewidth=1.0, linestyle="-") plt.plot(X, C, color="blue", linewidth=2.5, linestyle="--") # erster Graph # Plot sine with a green continuous line of width 1 (pixels) plt.plot(X, S, color="green", linewidth=1.0, linestyle="-") # zweiter Graph ##plt.plot(X, S, color="red", linewidth=2.5, linestyle="-") # Definition einer ausgefuellten Flaeche zwischen den Graphen plt.fill_between(X, C, S, where=C>S, facecolor = "green") # Modifikation der Plot-Umrandung, Verschiebung der Achsen in die Plot-Mitte ax = plt.gca() # gca stands for 'get current axis' ax.spines['right'].set_color('none') ax.spines['top'].set_color('none') ax.xaxis.set_ticks_position('bottom') ax.spines['bottom'].set_position(('data',0)) ax.yaxis.set_ticks_position('left') ax.spines['left'].set_position(('data',0)) # Set x limits ##plt.xlim(-4.0, 4.0) plt.xlim(X.min() * 1.1, X.max() * 1.1) # Set x ticks # Beschriftung mit LaTeX moeglich ##plt.xticks(np.linspace(-4, 4, 9, endpoint=True)) ##plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi]) plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], [r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$']) # Set y limits ##plt.ylim(-1.0, 1.0) plt.ylim(C.min() * 1.1, C.max() * 1.1) # Set y ticks plt.yticks(np.linspace(-1, 1, 5, endpoint=True)) ##plt.yticks([-1, 0, +1]) ##plt.yticks([-1, 0, +1],[r'$-1$', r'$0$', r'$+1$']) # Save figure using 72 dots per inch # savefig("exercice_2.png", dpi=72) # Show result on screen plt.show()
Ein schönes Beispiel für die Möglichkeiten von Matplotlib finden sie hier. Es handelt sich um die animierte Darstellung eines sogenannten Lorenz-Attraktors, der Lösung eines Satzes von Differentialgleichungen, die ein chaotisches Verhalten zeigt. Das Skript können sie direkt herunterladen und in der eigenen Python-Installation ausprobieren.
Graphen können in einem Python-Skript z.B. direkt nach der numerischen Bearbeitung von Daten automatisch generiert werden. Eine Alternative, insbesondere für die explorative und interaktive Datenauswertung und -darstellung, ist die für diese Zwecke optimierte Kommandozeile IPython, ein Ersatz für die Standard-Shell. IPython ist in der Anaconda Python Distribution vorkonfiguriert enthalten. Es gestattet ein interaktives Arbeiten in Kombination mit NumPy/SciPy/Matplotlib, das der kommerziellen Software MATLAB ähnlich ist. Der Aufruf erfolgt in der Windows-Eingabeaufforderung mittels jupyter console.
Eine andere Möglichkeit zur Interaktion mit Python, die sich insbesondere in der wissenschaftlichen Community immer weiter durchsetzt, besteht in den sog. Jupyter-Notebooks, die sich aus IPython entwickelt haben. Auch diese Möglichkeit ist mit Anaconda vorinstalliert. Jupyter-Notebooks bieten eine einfache Möglichkeit, eine interaktive Python-Sitzung inklusive der erzeugten Ausgaben und eventueller Kommentare abzuspeichern und auszutauschen. Der Aufruf von Jupyter in der Windows-Eingabeaufforderung erfolgt durch die Eingabe von jupyter notebook. Daraufhin öffnet sich ein Browserfenster, von dem aus eine ipynb-Datei eingelesen oder eine neue erstellt werden kann.
Eine hervorragende Informationsquelle für die Verwendung von Python, IPython und insbesondere Jupyter im wissenschaftlichen Kontext ist das Python Data Science Handbook von Jake VanderPlas. Der komplette Inhalt des Buches steht auch als eine Kollektion von Jupyter-Notebooks zur Verfügung, die Sie hier online lesen und unter diesem Link auch für die interaktive Beschäftigung herunterladen können (Knopf rechts oben „Clone or Download“, dann „Download ZIP“).
Aufgaben bis zum nächsten Mal¶
Versuchen Sie, mit Matplotlib die folgende Grafik zu erzeugen.
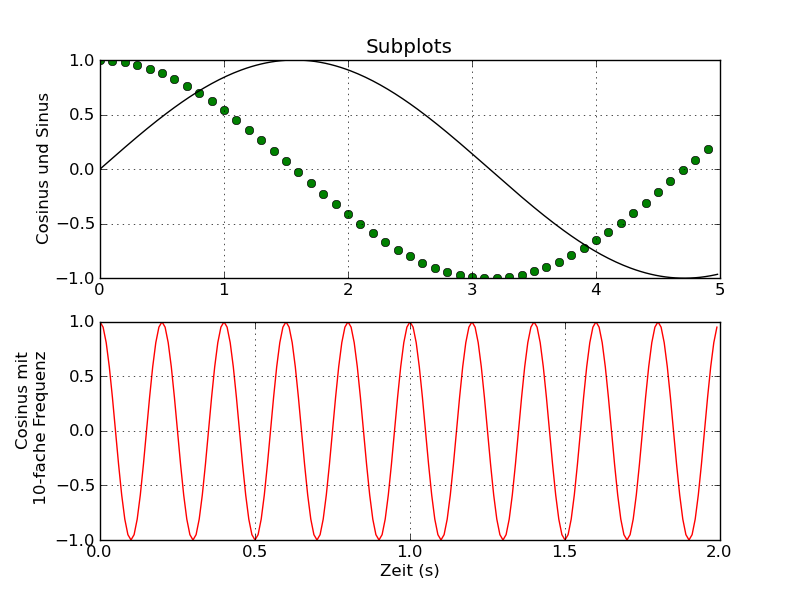
Informieren Sie sich dazu zum Subplot-Befehl!